A vártnál több megoldást küldtök, ennek természetesen nagyon örülünk, viszont így lemaradtam a válaszok átnézésével. Már első nap is érkeztek mesterséges intelligenciát használó megoldások, az első programozós megoldás az érmés feladatra jött (sikeresen le is futott).
Készült egy poszt a visszajelzéseknek, itt szívesen fogadunk mindenféle javaslatot, észrevételt.
Áramszünet
Általában nem örülünk, ha az óráink különböző időpontokat mutatnak, a következő feladatban viszont éppen ez segíthet nekünk.
Amikor Luca reggel elindult az iskolába, mindhárom órája a pontos időt mutatta. Napközben azonban egyszer áramszünet volt, így amikor délután hazaérkezett, a falióra negyed ötöt, a rádió órája 16:25-öt, az asztalán lévő digitális óra pedig 14:40-et mutatott.
Az áramszünet a falióra működését nem befolyásolja, viszont a digitális óra és a rádió órája kikapcsol, és amikor visszajön az áram, akkor a rádió órája 12:00-tól újraindul, míg a digitális órája attól az időponttól halad tovább, ahol az áramszünet kezdetekor leállt.
Mond Ryan – neves grafikus – olyan rajzokkal kísérletezik, amelyeket egyetlen szakaszláncolattal (töröttvonallal) hoz létre. Éppen hatszakaszos korszakát éli. Észrevette, hogy minél több háromszög jelenik meg egy-egy képén, annál több pénzért sikerül azt eladnia. A nem átfedő háromszögeket számolta, amik belseje üres, nem szeli át másik vonal. Sikerült már ötháromszöges grafikákat alkotnia, de itt nem állna meg.
Próbálj 6-szakaszos töröttvonallal minél több háromszöget létrehozni, hogy ihletet meríthessen belőle a mester! Hányat sikerült?
Példaként két korai Mond Ryan alkotás négy, és egy öt szakasszal:
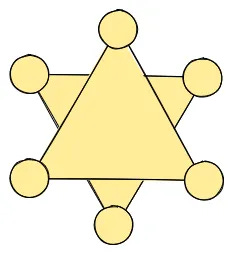
Először helyezzünk egymásra két szabályos háromszöglapot úgy, hogy azok szabályos hatszögben messék egymást. Majd hat körlapot rakjunk le, hogy a körök középpontjai a háromszögek csúcsaiban legyenek. Így éppen egy seriffcsillagot kapunk:
Egy háromszöglap területe 36 egység, egy körlap területe pedig 4 egység. Hány egység a csillag területe?
Megoldás
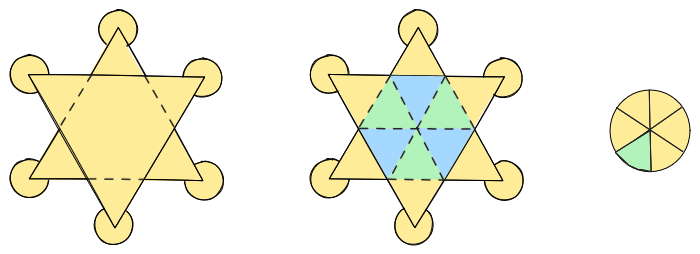
Nézzük meg a csillagot hátulról:
Kössük össze a szabályos hatszög csúcsait, ahogyan ez a középső ábrán látható. Így szabályos háromszögeket kapunk, ezek oldalai megegyeznek. Kilenc kis háromszögből áll egy nagy háromszög, vagyis a kis háromszögek területe 4 egység. Így a csillag területe összesen 36+3×4 = 48 egység.
A csillagot még kiegészítik a körlapok is. A jobb oldali ábrán láthatjuk, hogy egy körlapon egy-egy 60 fokos körcikk esik a háromszögre, ez éppen a körlap területének hatoda. A körlapok maradék 5/6-a növeli a területet, így a körlapok 20 egységgel járulnak hozzá a területhez.
Tehát a teljes terület 68 egység.
Madagaszkári érmék (*)
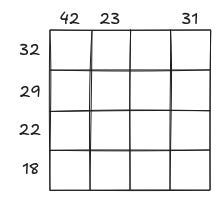
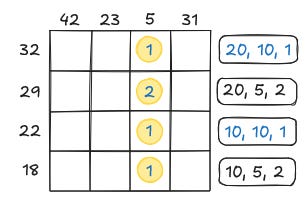
Madagaszkáron az 1, 2, 5, 10, 20 és 50 ariary-s érmék vannak forgalomban. Helyezzünk 1-1 érmét minden mezőre úgy, hogy a sorokban és az oszlopokban a számok azt jelöljék, hogy mennyi az ottani ariary-k összértéke!
Megoldás
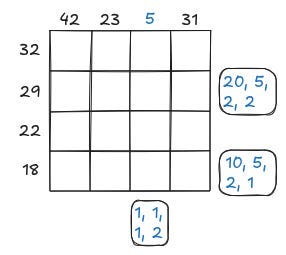
Mivel tudjuk mind a 4 sorban az érmék összegét, ezért a táblázatban lévő érmék összege: 32+29+22+18=101. Ekkor a harmadik oszlopban lévő érmék összege: 101-42-23-31=5. Néhány sorban és oszlopban meg tudjuk határozni, hogy pontosan milyen érmékből tudjuk kirakni az adott összeget. Ezeket írjuk a sorok és oszlopok mellé:
Látható, hogy a második sor harmadik mezője csak 2-es lehet. Emiatt a harmadik oszlop többi mezőjébe 1-esnek kell jönnie. Ennek ismeretében az első és a harmadik sorról is meg tudjuk mondani, hogy milyen érmékre bomlik fel az összeg.
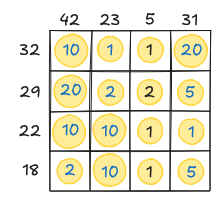
A negyedik oszlopot 31-re kétféleképpen lehet felbontani. Ha 10+10+10+1 arányban bontjuk fel, akkor a 2. sorba nem tudnánk mit tenni, így azt az oszlopot csak 20+5+5+1 módon tudjuk felbontani, aminél a számok csak 20, 5, 1, 5 sorrendben követhetik egymást. A 23 a maradék lehetőségek közül csak 10+10+2+1 módon bontható fel, 1, 2, 10, 10 sorrendben. Innen pedig már az első oszlop is egyértelműen kitölthető.
Így a kérdőíven szereplő kérdésre a válasz 10, 2, 1, 5.
Mond Ryan feladatában a legelsö példát 2 vagy 3 háromszögnek számoljuk-e?
Mond Ryan feladatában az elfajuló háromszögeket is háromszögeknek tekintjük? Ahol két szakasz összege megegyezik a harmadik szakasszal stb.