minden·ki·jön – 6. nap

A bőrönd zárja · Mire gondoltam? | Janus arcú légió · Szaloncukrok

Újabb hét, újabb feladatok. Arra gondoltunk, hogy mostantól segítségeket is írunk a feladatokhoz: a nap folyamán valamikor kommentben tesszük közzé őket a honlapon. Aki ennek ismeretében szeretne gondolkodni, bátran keresse ott!

Az elmúlt héten összesen 500-an küldtetek be megoldást, átlagosan 4 feladatra. Igyekszünk mindent feldolgozni, egyelőre még nem teljesen értünk a végére.

A bőrönd zárja, avagy a magáról árulkodó szám

Szuperbiztonságos bőröndömet tízjegyű számzárral látták el. 0-tól 9-ig állíthatom minden számát. Boldogan vittem haza a boltból, de hamarosan eszembe jutott, hogy a szupertitkos számomat majd meg is kellene jegyeznem anélkül, hogy felírnám valahova. Remek ötletem támadt. Úgy állítom be a nyitó kódot, hogy a számsor árulkodjon magáról:

Az első szám azt árulja el, hogy hány 0 van a számsorban, a második azt, hogy hány 1-es, a harmadik, hogy hány 2-es, … a tizedik, hogy hány 9-es. Ezt biztosan nem felejtem el, csak el ne áruljam senkinek.

Mi lehet a záram kódja?

Andi csatlakozó kérdése: Andi azt mondja, ő biztosan nem bíbelődne a reptéren egy tíz hosszú számsorral, így felmerült benne, hogy melyik a legkisebb magáról árulkodó szám. Szerinted melyik?

Mire gondoltam?

Gondoltam egy számot 1-től 10-ig. Egy kérdésben választhattok egy számot, amiről elárulom, hogy közel van-e a gondolt számhoz. Mit jelent az, hogy közel van? Azt, hogy a két szám vagy megegyezik, vagy szomszédosak (azaz a különbségük maximum 1).

Találjátok ki a gondolt számot! Ha kitaláltátok, akkor próbáljátok meg minél kevesebb kérdéssel! (Online is ki tudjátok próbálni.)

Janus arcú légió

Az ókori Rómában Janus légiója 50 katonából állt, akik 10×5-ös téglalap alakban helyezkedtek el. Tudjuk, hogy a katonák mindegyike igazmondó vagy hazug volt. Egyszer mindegyikük a következő kijelentést tette: „Azok a társaim, akikkel egy sorban vagy egy oszlopban vagyok, azok mindegyike hazug.”

Hány igazmondó volt a légióban?

Megoldás

Egy sorban maximum egy igazmondó lehet, hiszen ha többen lennének, akkor nem mondanának igazat. Tehát maximum öt igazmondó lehet.

Ha egy hazug állít egy ilyen mondatot, akkor kell találnunk legalább egy igazmondót vele egy sorban vagy oszlopban. Ezt meggondolva azt is látjuk, hogy minden sorban lennie kell igazmondónak. Hiszen, ha lenne egy csupa hazug sor, akkor ennek a sornak és egy csupa hazug oszlopnak a metszetében lévő ember hazug lenne, ezért ő nem mondhatná el a fenti mondatot. Csupa hazug oszlopnak biztosan lennie kell, hiszen 10 oszlop van, és maximum 5 igazmondó.

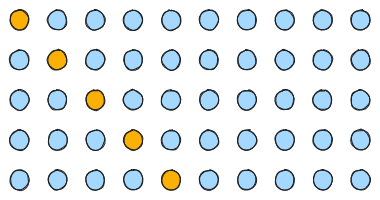
Tehát az igazmondók száma sem több, sem kevesebb nem lehet 5-nél. Erre tudunk példát is mutatni, naranccsal jelölve az igazmondókat. Annak meggondolását az Olvasóra bízzuk, hogy ebben a konstrukcióban mindenki valóban elmondhatta a feladatban szereplő állítást.

Szaloncukrok (**)

Az iskolai karácsonyi ünnepségre a szülők 100 szaloncukrot küldtek a gyerekeknek egy nagy zsákban. Azonban azt nem árulták el a diákoknak, hogy hány különböző ízesítésű cukrot vettek. Annyit viszont elmondtak, hogy minden típusból ugyanannyit küldtek. Legkevesebb hány szaloncukrot kell elfogyasztaniuk a diákoknak ahhoz, hogy biztosan (szerencse nélkül) meg tudják mondani, hogy hány különböző ízesítésű (típusú) szaloncukor van a zsákban?

Megoldás

Érdemes úgy gondolkozni a feladaton, hogy ha minél tovább szeretnénk eltitkolni a különböző ízesítések számát, akkor hogyan kellene adni a gyereknek a szaloncukrokat.

Nézzünk először egy egyszerűbb példát, legyen most csak 12 szaloncukor. Az első 5 szaloncukor ízesítése: 1, 1, 1, 2, 3. (Az egyszerűség kedvéért számozzuk meg az ízeket.) Meg lehet-e ebből mondani, hogy hány különböző van? Sajnos még nem, mert lehet, hogy csak ez a 3 íz van, mindegyikben 4 cukorral, de az is lehetséges, hogy 4 íz van és mindegyikből 3 cukor.

Mi a helyzet akkor, ha az első 5 cukor mind különböző ízesítésű? Sajnos még akkor sem tudjuk megmondani, mert az is lehet, hogy 6 különböző íz van, 2-2 cukor mindegyikből, de az is lehet, hogy 12 különböző ízű cukor van a zsákban. De az nem lehet, hogy 5 különböző íz van csak, mert akkor nem lehetne mindegyikből ugyanannyi, hiszen 12 nem osztható 5-tel.

Térjünk vissza az eredeti feladathoz. Elképzelhető, hogy a gyerekek már megettek 80 szaloncukrot, és még mindig nem derült ki az igazság. Ha 4 különböző ízből pontosan 20 darab cukrot kaptak, akkor még mindig két lehetőség van:

1. Lehet, hogy összesen 4 íz van, mindből 25-25 darab.

2. De az is lehet, hogy 5 különböző íz van, és a zsákban még éppen 20 darab van egy olyan ízből, amiből eddig még nem is ettek.

Most jön a megoldás nehezebb része, amikor megmutatjuk, hogy 81 szaloncukor elfogyasztása után már biztosan ki tudjuk találni, hogy hány különböző ízesítés van.

Gondoljuk meg azt, hogy mikor lehet két különböző, 100 szaloncukorból álló zsákot összekeverni. Legyen az egyik esetben x, a másik esetben y íz (legyen x < y). Mivel minden ízből ugyanannyi cukor van, ezért x és y is osztója a 100-nak. Keressük meg, hogy ekkor mennyi az a legtöbb szaloncukor, ami kivehető a zsákból, úgy, hogy még ne tudjuk eldönteni, hogy x vagy y íz van. Tegyük a különböző ízeket, különböző dobozokba.

• Hány dobozt használhatunk? Maximum x-et, hiszen, ha ennél több lenne, akkor x-nél több íz lenne a zsákban.

• Egy dobozba hány cukrot tehetünk? Maximum 100/y-t, hiszen ha egy dobozba ennél több cukor jutna, akkor az azt jelentené, hogy y-nál kevesebb íz van.

A két megfigyelés együtt azt mutatja, hogy maximum x · 100/y cukrot vehetünk ki úgy, hogy még ne tudjuk eldönteni, hogy hány íz van, hiszen maximum x dobozt használhatunk, és egy dobozba maximum 100/y cukrot tehetünk.

Vagyis az x és y íz lehetőségét, akkor tudjuk összekeverni, ha maximum x · 100/y cukrot veszünk ki a zsákból. Ezt az értéket maximalizálni szeretnénk, tehát olyan osztókat keresünk, ahol az x/y érték a lehető legnagyobb. Ha x rögzített, akkor ez a hányados akkor maximális, ha y a lehető legkisebb (de még nagyobb x-nél), így elég csak szomszédos osztókat vizsgálnunk.

A 100 osztói: 1, 2, 4, 5, 10, 20, 25, 50, 100. A szomszédosak hányadosa rendre: 1/2, 1/2, 4/5, 1/2, 1/2, 4/5, 1/2, 1/2. Ezek közül a legnagyobb a 4/5 és 4 · 100/5 = 80, ami a fenti gondolatmenet alapján már bizonyítja, hogy 81 elfogyasztott szaloncukor esetén már biztosan nem lehet kétség az ízek számát illetően.

(Mivel a 80 kétszer is szerepel a sorozatban, így 80 elfogyasztott szaloncukor esetén még két különböző esetben sem lehetünk biztosak az ízek számában. A fent már említett 4, illetve 5 íz esetének megkülönböztethetetlensége mellett a 20 és 25 íz megkülönböztetéséhez is 81 szaloncukorra van szükség.)

Megjegyzés: 100 szaloncukor esetén az derült ki, hogy a cukrok több mint 80%-át kell kivenni a zsákból. Tudtok olyan példát mutatni, ahol 99%-nál is többet kell kivennünk?