Nagyon örülünk, hogy sokféle megoldást küldtetek. Egyelőre az első hetet néztük meg valamennyire, készítettünk belőle egy válogatást is, ha van kedvetek, akkor nézzétek meg.
Tarkal papa kendője (*)
Tarkal papa 4 lányunokájának szeretne pöttyös selyemkendőt varrni. Tudja, hogy a hagyományos kendő szabásmintája egyenlő szárú derékszögű háromszög alakú, és minden unokának más méret kell. A méteráruboltból hazaérve azonban döbbenten veszi észre, hogy félreértették, és egyetlen nagy négyszög alakú anyagot kapott. Rövid gondolkodás után a fejére csap, hiszen rájön, hogy fel tudja vágni az anyagot úgy, hogy mind a négy kendő kijöjjön belőle, és még csak nem is kell belőle semmit kidobni!
Hogyan nézhetett ki az anyag, amit Tarkal papa hazavitt?
(Más szóval: Mutassatok olyan négyszöget, amelyet 4 különböző méretű egyenlő szárú derékszögű háromszögre lehet bontani. A beküldendő kérdés a négyszög legrövidebb, egységhosszú oldalával szemközti oldal hossza, de természetesen ábrának is örülünk.)
Egyre jobb kérdések (**)
Gondoltam egy számot 1-től 14-ig. Körönként választhattok egy számot szintén 1-től 14-ig. A második körtől kezdve elárulok annyit, hogy a választott szám közelebb van-e a gondolt számhoz, mint az előző körben választott. (Ha véletlenül a gondolt számra kérdeztek, akkor is csak annyit árulok el, hogy közelebb van, mint az előző választás.)
Határozzátok meg a gondolt számot! Próbáljátok meg minél kevesebb kérdéssel!
Írjatok minden mezőbe egy számot úgy, hogy egy N nagyságú régióban 1-től N-ig minden szám pontosan egyszer szerepeljen. Ezenkívül két azonos szám ne érintse egymást még átlósan sem.
Megoldás
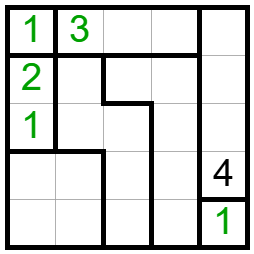
Az 1 nagyságú részekbe a szabály szerint beírható az 1-es. Innen kiindulva még néhány szám beírható:
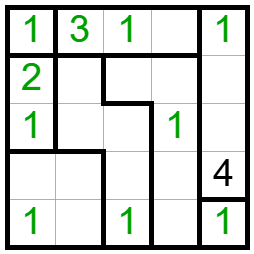
A felső sorban a 3-as mellé jön még az 1-es és 2-es, így az ez alatt lévő két mezőbe nem jöhet se 1-es, se 2-es. Így abba a régióba már egyértelműen beírható az 1-es, majd onnan a többi is:
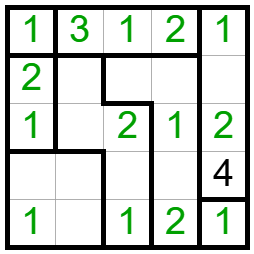
Ezek után a 2-esek közül írható be néhány darab:
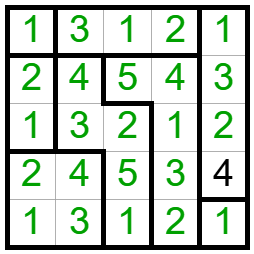
Most a hármasokból tudunk néhányat beírni, onnan pedig már könnyen befejezhető a kitöltés:
Ez alapján a kérdésre a válasz: 1, 4, 2, 4, 1.
Themisz-parton (*)
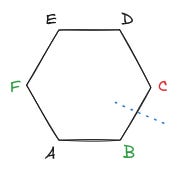
A Themisz-folyó egyik partján igazmondók, a másikon hazugok élnek. Prof. Dialektosz, a neves néprajzkutató, egyik útja során beszélgetett hat helybélivel, akik egy szabályos hatszög csúcsaiban laknak. Feljegyezte, mit mondtak, ám sajnos elfelejtette, melyik oldalon vannak az igazmondók és melyiken a hazugok. Sőt, még azt sem találja a jegyzeteiben, hogy pontosan hol szeli át a hatszöget a folyó egyenes szakasza.
Az anonimitás jegyében A, B, C, D, E, F betűkkel jelölte a lakókat, akik ilyen sorrendben laknak a hatszög szomszédos csúcsaiban. Ők a következőket állították:
A: D és E nem egy oldalon élnek.
B: F-fel ugyanazon az oldalon lakom.
C: F hazug.
D: B-vel ugyanazon az oldalon lakom.
Segíts kitalálni Prof. Dialektosznak, hogy ki mond igazat és ki hazudik!
Megoldás
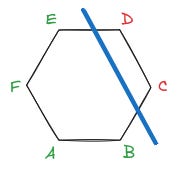
Vegyük észre, hogy B nem lehet hazug, hiszen D akár igazat mond, akár hazudik, az ő állítása alapján B mindenképpen igazmondó. Ugyanez vonatkozik F-re is B állítása alapján. Viszont ebből következik, hogy C biztosan hazug, így tehát a folyó áthalad a hatszög B és C közötti oldalán.
Mivel a folyó egyenes, A mindenképpen igazmondó, ő pedig azt állítja, hogy D és E a folyó különböző oldalán laknak. Ismét kihasználjuk, hogy a folyó egyenes, és ezzel megtaláljuk az egyetlen megoldást:
Némi zavart érzek a nyelvtanban ennél a mondatnál: „A beküldendő kérdés a négyszög legrövidebb, egységhosszú oldalával szemközti oldal hossza”. Miért kell kérdést beküldeni? Minek az egysége az az egységhosszú oldal? Valamelyik kendőé?
Némi zavart érzek a nyelvtanban ennél a mondatnál: „A beküldendő kérdés a négyszög legrövidebb, egységhosszú oldalával szemközti oldal hossza”. Miért kell kérdést beküldeni? Minek az egysége az az egységhosszú oldal? Valamelyik kendőé?
Segítségek a mai feladatokhoz (a segítségeket erre a kommentre írom meg válaszul):