A hét utolsó két feladata érkezik, legközelebb kedden fogunk újabb levelet küldeni. Ha van kedvetek, akkor gondolkozzatok a korábbi feladatokon, ezeket itt találjátok. Ezekre a feladatokra is szívesen fogadunk megoldásokat, bátran küldjétek be azokat is.
Kötögetés
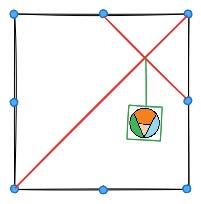
A PictArt cég piacra dobta legújabb termékét, egy DIY alapú képkeretet. Ez egy négyzet alakú, fából készült üres keret, melyen 8 rögzítési pont van: a keret csúcsaiban és az oldalfelező pontokban. A csomagban kapunk 4 impozáns zsinórt is, melyeket a rögzítési pontok közé tudunk kifeszíteni, egy pontba csak egy zsinórvég rögzíthető. Ezután a zsinórok metszéspontjaiba akaszthatunk egy-egy képet egy erre kialakított kampó segítségével. (Ha kettőnél több zsinór is egy pontban metszi egymást, sajnos oda is csak egy kampót rögzíthetünk, tehát csak egy képet tudunk rá felakasztani.) Maximum hány képre elég ez a keret, azaz hány metszéspontja lehet a zsinóroknak?
Törtek törtje (**)
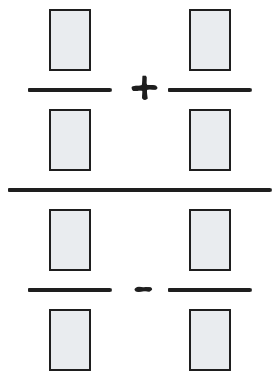
Az 1, 2, 3, ..., 8 számokat kell elhelyezni az alábbi kifejezésben. Keressetek olyan elrendezést, hogy minél nagyobb legyen a tört értéke! Biztosak vagytok benne, hogy megtaláljátok a legnagyobbat? (Nullával nem oszthatunk.)
Tarkal papa kendője (*)
Tarkal papa 4 lányunokájának szeretne pöttyös selyemkendőt varrni. Tudja, hogy a hagyományos kendő szabásmintája egyenlő szárú derékszögű háromszög alakú, és minden unokának más méret kell. A méteráruboltból hazaérve azonban döbbenten veszi észre, hogy félreértették, és egyetlen nagy négyszög alakú anyagot kapott. Rövid gondolkodás után a fejére csap, hiszen rájön, hogy fel tudja vágni az anyagot úgy, hogy mind a négy kendő kijöjjön belőle, és még csak nem is kell belőle semmit kidobni!
Hogyan nézhetett ki az anyag, amit Tarkal papa hazavitt?
Megoldás
Ragasszuk össze Tarkal papa négyszögét egyenlő szárú derékszögű háromszögekből! Helyezzük el az elsőt, majd a következő háromszög egyik befogóját ragasszuk az előző átfogójához! Ezt kétféleképpen tehetjük meg, de a megoldás szempontjából nem lényeges, hogy melyiket választjuk, mert a két kendőkezdemény egymás tükörképe lesz.
Ha ezt folytatjuk, biztosan nem lesznek ugyanakkorák a háromszögeink, hiszen egyre nagyobbakat ragasztunk, azonban négy háromszög elhelyezése után a végeredmény még nem biztos, hogy négyszög lesz.
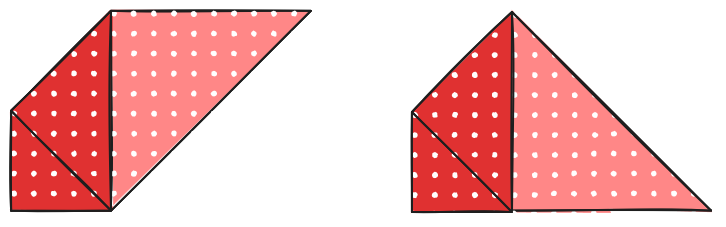
A harmadik háromszög ragasztásánál ismét választás elé kerülünk aszerint, hogy melyik befogót ragasztjuk a második átfogójához. A két lehetőség:
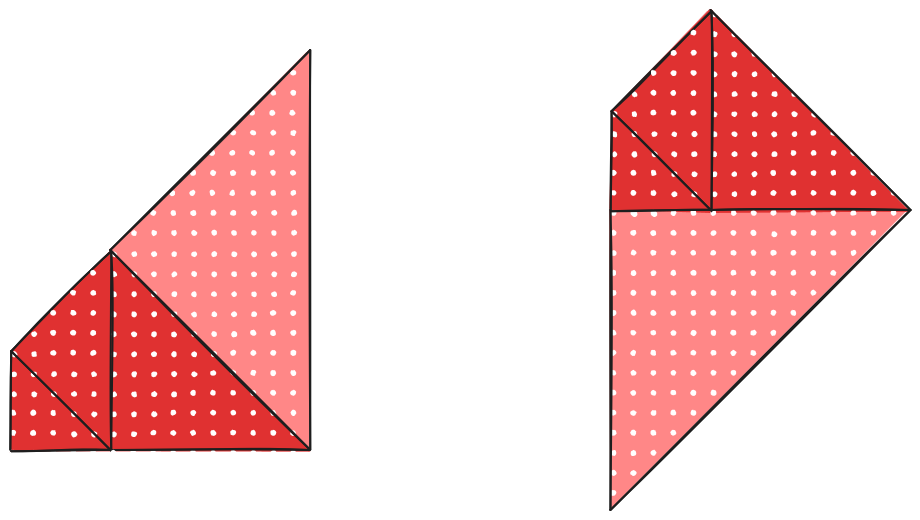
Innen már csak egy lépésre van szükségünk, a jobb oldali ábra két lehetséges befejezését mutatjuk meg: Az egyik esetben 4 (bal oldali ábra), a másikban 3 egység lesz a szemközti oldal hossza.
Ti is ezt a két példát találtátok, mi nem tudjuk, hogy van-e még.
Egyre jobb kérdések (**)
Gondoltam egy számot 1-től 14-ig. Körönként választhattok egy számot szintén 1-től 14-ig. A második körtől kezdve elárulok annyit, hogy a választott szám közelebb van-e a gondolt számhoz, mint az előző körben választott. (Ha véletlenül a gondolt számra kérdeztek, akkor is csak annyit árulok el, hogy közelebb van, mint az előző választás.)
Határozzátok meg a gondolt számot! Próbáljátok meg minél kevesebb kérdéssel!
Megkaptuk az első pull request-et, köszönjük.
Megoldás
Sokféle módon el lehet indulni a feladatban. Természetes elindulás, hogy 1-től kezdve végigkérdezzük a számokat, ekkor egy ideig közelebb választ kapunk, ez egy idő után nincs közelebbre vált. A gondolt szám a váltásnál lesz. Ez 14 kérdés.
Javíthatunk ezen, ha nem egyesével, hanem kettesével vagy hármasával megyünk végig (és a váltás környékén tisztázzuk a kérdéses eseteket). Így 7 kérdéssel is lehet találni a gondolt számot.
A további javítás előtt gondoljuk meg, hogy minimum hány kérdésre van szükségünk. Az első kérdésben nem kapunk információt, minden további kérdésnél kétféle választ kaphatunk. Így lehetséges válaszsorozatok száma minden kérdésnél megduplázódik. Vagyis minimum 5 (1+4) kérdés szükséges, hiszen ekkor 16 különböző válaszsorozat érkezhet, amely már elvileg elegendő a 14 lehetséges szám megkülönböztetéshez.
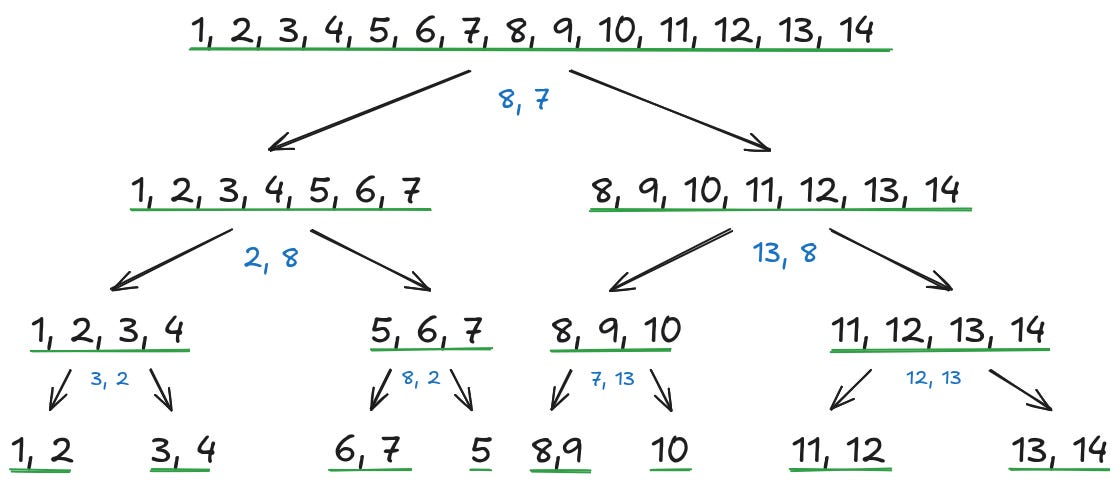
Nézzük meg, hogy 5 kérdéssel ki tudjuk-e találni a gondolt számot. Az alsó becslés alapján érdemes megpróbálkozni azzal, hogy felezzük a gondolt szám potenciális helyeit. Kezdjünk például a 7-tel és a 8-cal. Ez valóban be is fejezhető, ennek a – kicsit pepecselős – részleteit mutatja a következő ábra. Az ábrán aláhúzással jelöltük a potenciális gondolt számok lehetséges halmazát. A kék számok jelzik azt, hogy mi volt az aktuális és az azt megelőző körben választott számunk (az ötödik kör meggondolását a kedves Olvasóra bízzuk).
Ezzel megoldottuk a feladatot, hiszen korábban beláttuk, hogy 4 kérdés semmiképpen sem elég.
A konkrét eset kijött, valami hiányérzet maradhat bennük. Mi a helyzet általában? 15 számhoz is elég 5 kérdés? És 16-hoz? Általában meg tudjuk mondani, hogy n kérdés meddig elég? Ezekre a kérdésekre egyelőre nem tudunk pontosan válaszolni, ha van kedvetek, gondolkozzatok rajta. Elképzelhető, hogy a megoldás nem olyan szép.
Ha úgy módosítunk a feladat feltételein, hogy a kérdezett szám az intervallumon kívül is lehet (tehát lehet például -2-t is kérdezni), akkor létezik szép válasz.







Segítségek a mai feladatokhoz (a segítségeket erre a kommentre írom meg válaszul):